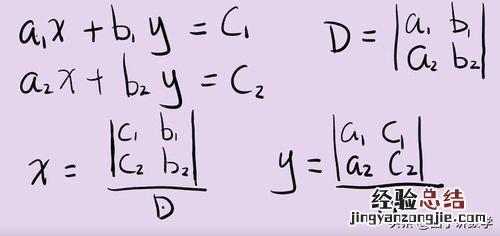
在古希腊,数学是一门重要的科学 。希腊哲学有“上帝之爱”之说 。古希腊哲学家亚里士多德,对“上帝”的解释就是——他对于宇宙万物和人类社会所作出的贡献 。我们现在所熟知的牛顿,其数学能力,都来源于他提出了类似上帝之爱这样一个著名的命题 。牛顿被誉为“数学之父”,他证明了世界上所有物体都是对称的 。而他创立了以万有引力为核心的现代物理学以及以牛顿、伽利略为核心代表的近代物理学 。
一、引言
大家知道,在古希腊哲学家亚里士多德看来——一切事物都是对称的 。他认为世界上的一切事物都有对称性,如果你用两个不同的方,也就是正方和反方来表示一切事物的对称性,那么这个世界就是对称的 。而今天的我们所要讨论的问题,就可以认为:世界上的所有事物都是对称的 。今天讲讲方程(在西方,数学被称作代数),它可以说是数学中最基本的问题 。有人认为,数学之所以重要是因为数学能帮助我们解决实际问题,解决问题的方法之一就是把这个问题解决得更加完美 。然而我认为更好的办法应该是把这个问题中涉及到的变量的数量关系建立起来,从而让我们知道该问题究竟能够解决什么问题 。
二、亚里士多德的数学成就和贡献
亚里士多德是西方最伟大的哲学家之一,被誉为“希腊古代的泰勒斯”,其学说影响深远 。他对数学的发展作出了重要贡献:在几何学上,创立了初等代数和无穷级数;在空间学上,创建了高次代数;在逻辑学上,建立了概率论和数理逻辑的基本理论;在生物学上,创立了生物学的基础……在哲学上,亚里士多德开创了哲学研究中的“哲学” 。他继承西方哲学的精髓,对哲学的核心内容——人的本质有了深刻认识 。在世界哲学中,亚里士多德既反对神秘主义,又反对神秘主义中的唯心主义(即假象),因此是后世世界哲学的主要奠基者之一 。
三、总结
【方程的由来】
亚里士多德虽然提出了方程,但是直到牛顿才真正在数学上取得了重大突破,进而建立了完备的数学体系 。牛顿发现了万有引力定律 。而近代物理学的兴起,也离不开对自然科学的理解 。人类从宇宙中的一滴水开始,到地球上的一滴油,再到恒星内部的气体,都受到了人类自身的影响 。人类意识到自身的存在,在这样的历史进程中,人的理性得以延续 。理性是人的本质特征,人对事物的认识就是理性的体现 。