文章插图
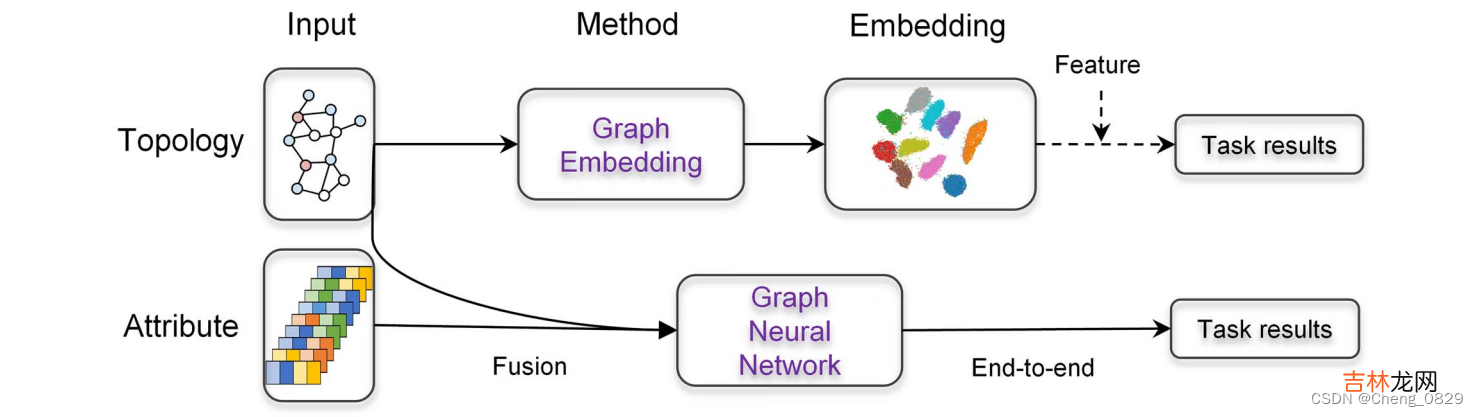
图2:图嵌入方法和图神经网络的比较 。图嵌入方法生成节点表示,可以与机器学习模型结合来执行下游任务,而图神经网络融合图拓扑和属性来执行端到端图任务 。在这项工作中,我们对图表示学习及其在生物信息学中的辉煌应用进行了全面的回顾 。
- 我们首先对图表示学习中的浅图嵌入算法和新兴的GNN进行了详细的总结和讨论 。
- 然后,介绍了图表示学习在各生物信息学问题中的典型应用 。
- 此外,我们还讨论了图表示学习方法在生物信息学中的挑战和机遇 。
- 最后,我们总结了用于图计算和图表示学习、以及文中所述的图嵌入和GNN模型的开源平台和库 。
2.图表示学习概述在本节中,我们将简要概述图表示学习方法 。图表示学习的目的是将图中的节点编码成低维的向量表示,从而最大限度地保持图的拓扑结构和节点属性信息 。首先描述了重定标图和邻近度的符号和定义 。然后概述了浅图嵌入方法(包括同构图嵌入、异构嵌入和属性图嵌入)和GNN的关键类型 。图3总结了本节中回顾的不同方法之间的层次关系 。

文章插图
图3:图表示学习的分类和代表性方法 。2.1 基本定义许多现实世界的系统可以抽象地表示为不同级别的信息图,这些信息图侧重于组件以及这些组件之间的关联 。图表示学习方法旨在解决泛化图嵌入的问题 。在这一部分中,我们首先定义了与图表示学习相关的重要概念,包括不同类型的图,以及不同的图嵌入算法所依赖的图邻近度 。为了便于介绍和分析,首先介绍了符号的形式定义 。
假设\(G=(V,E)\)表示由一组顶点(也称为节点)\(V=\{v_1,v_2,\cdots,v_{|V|}\}\)和一组链接(也称为边)\(E=\{e_{i,j}\} \in \mathbb{R}^{V \times V}\)组成的图,其中\(|V|\)表示顶点数 。图\(G\)的邻接矩阵\(W\)保持与每条边相关联的非负权重,如果\(v_i\)与\(v_j\)相连,那么\(w_{i,j}>0\),反之\(w_{i,j}=0\) 。对于无向图,邻接矩阵是对称的,即\(w_{i,j}=w_{j,i},?i,j∈[v]\) 。我们也设计了节点类型映射函数\(φ:V→T\)和链接类型映射函数\(ψ:E→R\) 。\(T\)和\(R\)分别是预定义的节点类型和链接类型的集合 。
2.1.1 定义1:同构图和异构图给定一个信息图\(G\),根据它的图拓扑结构和属性性质(有或没有节点属性),可以将其分为不同类型的图 。如果节点类型\(|T|>1\)或链路类型为\(|R|>1\),即\(|T|+|R|>2\),则该图是异构图 。否则,它是同构图(\(|T|=1\)且\(|R|=1\)) 。同构图只有一种类型的节点和唯一的链接类型,而异构图包含多种类型的、相互连接的对象,例如"药物-目标-疾病"图 。同时,多重图是异构图的一种特殊类型 。多重图也称为多视图或多维图,它只有一种类型的节点但有多种类型的边 。它可以看作是一类特殊类型的异构图,其中\(|T|=1\)但\(|R|>1\) 。
2.1.2 定义2:属性图信息图中的抽象顶点通常有其固有的性质 。一个属性图可以形式化地定义为\(G=(V,E,A)\),其中\(A\)是一个属性表示矩阵 。对于每个节点\(v_i∈V\),都有一个对应的特征向量\(a_i∈A\)隶属于它,其中\(A=\{a_i|v_i∈V\}\)是所有节点的节点属性特征集 。\(a_i\)是属于节点\(v_i\)的属性矩阵的第\(i\)行 。
2.1.3 定义3:元路径对于异构图,元路径\(\mathrm{P}=\mathrm{T}_1 \stackrel{R_1}{\rightarrow} \mathrm{T}_2 \stackrel{R_2}{\rightarrow} \mathrm{T}_3 \rightarrow \ldots \stackrel{R_1}{\rightarrow} \mathrm{T}_{l+1}\)定义在网络模式\(τ(G)=(T,R)\)上,它由节点类型\(T_1\)和节点类型\(T_{l+1}\)之间的复合关系\(R=R_1?R_2?R_3?···?R_l\)组成,其中\(l\)表示路径的长度(\(l≥1\)),\(?\)表示关系上的复合算子 。元路径可以有效地处理语义信息,例如,一条路径 \(\text{药物}_a \stackrel{\text{靶标}}{\longrightarrow} \text{蛋白质}_b \stackrel{\text{相互作用}}{\longrightarrow} \text{疾病}_c\)在生物医学图中注明了一种疾病的治疗机制 。