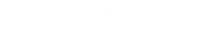初等数论学习笔记 III：数论函数与筛法(13) _生活百科

#include <bits/stdc++.h>using namespace std;using ll = long long;constexpr int N = 5e6 + 5;bool vis[N];int cnt, pr[N], mu[N], phi[N], smu[N];ll sphi[N];unordered_map<int, ll> p, m;ll dp(int n) {if(n < N) return sphi[n];auto it = p.find(n);if(it != p.end()) return it->second;ll sum = 1ll * n * (n + 1ll) / 2;for(int l = 2, r; ; l = r + 1) {r = n / (n / l);sum -= (r - l + 1) * dp(n / l);if(r == n) break;}return p[n] = sum;}int dm(int n) {if(n < N) return smu[n];auto it = m.find(n);if(it != m.end()) return it->second;ll sum = 1;for(int l = 2, r; l <= n; l = r + 1) {r = n / (n / l);sum -= (r - l + 1) * dm(n / l);if(r == n) break;}return m[n] = sum;}int main() {mu[1] = phi[1] = 1;for(int i = 2; i < N; i++) {if(!vis[i]) pr[++cnt] = i, mu[i] = -1, phi[i] = i - 1;for(int j = 1; j <= cnt && i * pr[j] < N; j++) {vis[i * pr[j]] = 1;if(i % pr[j] == 0) {phi[i * pr[j]] = phi[i] * pr[j];break;}phi[i * pr[j]] = phi[i] * (pr[j] - 1);mu[i * pr[j]] = -mu[i];}}for(int i = 1; i < N; i++) smu[i] = smu[i - 1] + mu[i], sphi[i] = sphi[i - 1] + phi[i];int T, n;cin >> T;while(T--) {cin >> n;cout << dp(n) << " " << dm(n) << "\n";}return 0;}参考文章第一章：