经验总结

  1. 首页 > 生活 > >

数据结构与算法【Java】08---树结构的实际应用( 三 )

生活百科

结果：

数据结构与算法【Java】08---树结构的实际应用

文章插图
2、赫夫曼树2.1、简介1、给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl) 达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树 。
2、赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近
重要概念和举例说明
  • 路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径 。通中分支的数目称为路径长度 。若规定根结点的层数为 1，则从根结点到第 L 层结点的路径长度为 L-1
  • 结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权 。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积
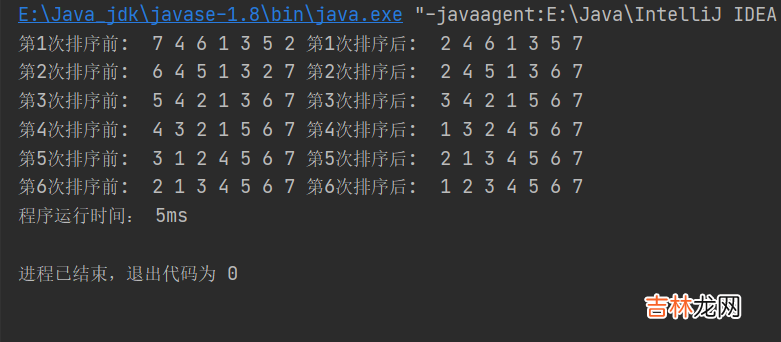
  • 树的带权路径长度：树的带权路径长度规定为 所有叶子结点的带权路径长度之和，记为 WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树 。
  • WPL 最小的就是赫夫曼树

数据结构与算法【Java】08---树结构的实际应用

文章插图
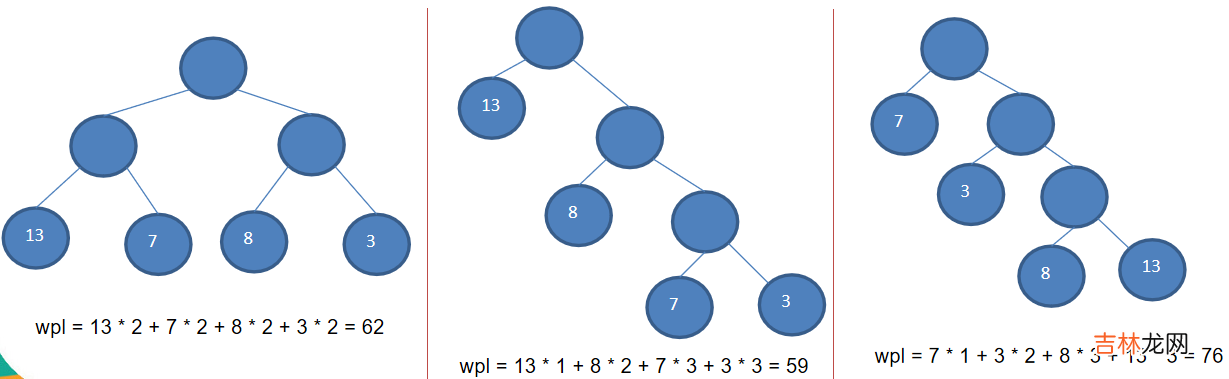
2.2、赫夫曼树创建思路图解给出一个数列 {13, 7, 8, 3, 29, 6, 1}，要求转成一颗赫夫曼树
构成赫夫曼树的步骤：
  1. 从小到大进行排序, 将每一个数据，每个数据都是一个节点 ，每个节点可以看成是一颗最简单的二叉树
  2. 取出根节点权值最小的两颗二叉树
  3. 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
  4. 再将这颗新的二叉树，以根节点的权值大小 再次排序，不断重复 1-2-3-4 的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
图解：
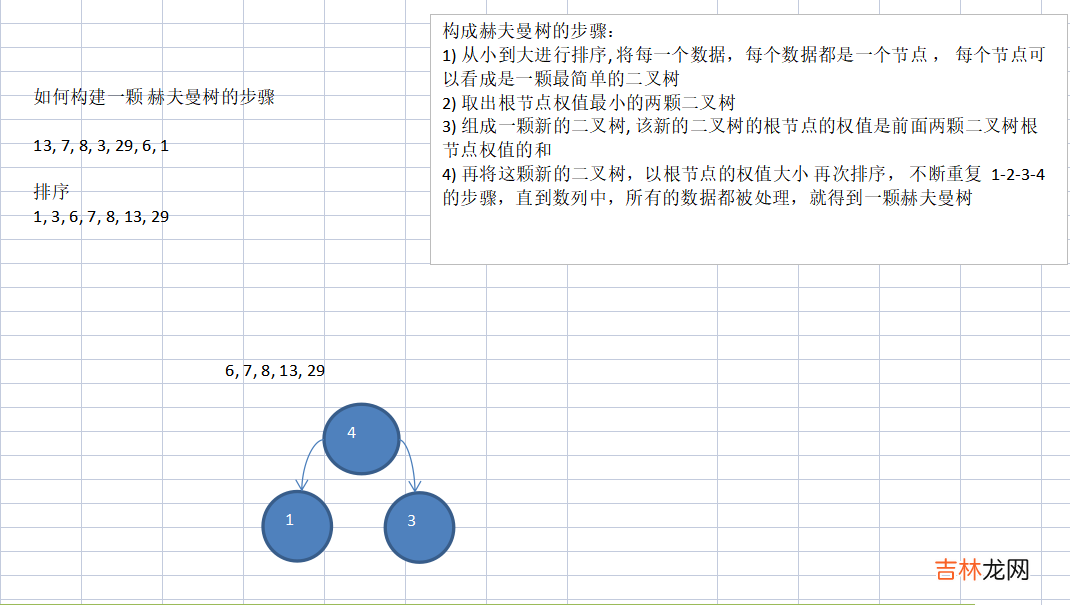
（1）选出最小的两个数组成二叉树
数据结构与算法【Java】08---树结构的实际应用

文章插图
（2）接下来在4,6,7,8...中选择最小的两个4，6(注意这里要加入第一步组成的节点4,大的在右边，小的在左边)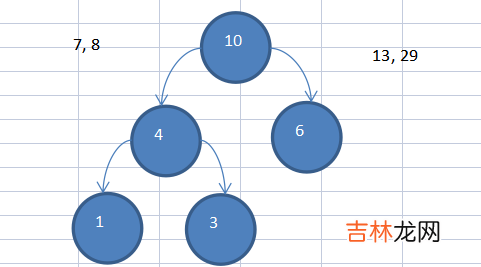
数据结构与算法【Java】08---树结构的实际应用

文章插图
（3）重复上述步骤
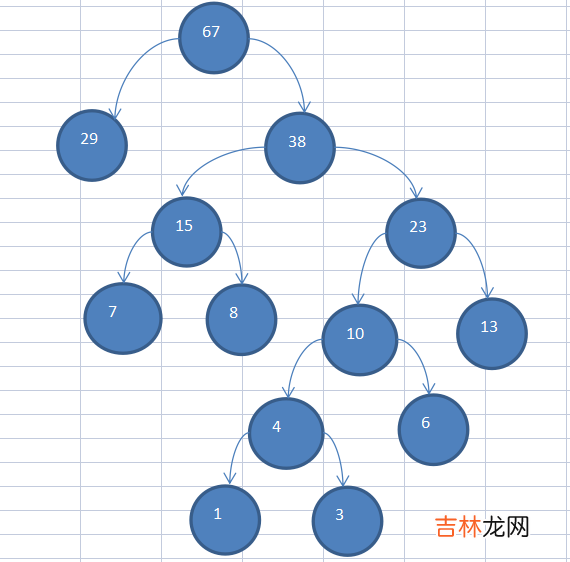
数据结构与算法【Java】08---树结构的实际应用

文章插图
2.3、赫夫曼树代码实现public class HuffmanTree {public static void main(String[] args) {int arr[] = { 13, 7, 8, 3, 29, 6, 1 };Node root = createHuffmanTree(arr);preOrder(root); //67,29,38,15,7,8,23,10,4,1,3,6,13}//编写一个前序遍历的方法public static void preOrder(Node root) {if(root != null) {root.preOrder();}else{System.out.println("是空树，不能遍历~~");}}// 创建赫夫曼树的方法/**** @param arr 需要创建成哈夫曼树的数组* @return 创建好后的赫夫曼树的root结点*/public static Node createHuffmanTree(int[] arr) {// 第一步为了操作方便// 1. 遍历 arr 数组// 2. 将arr的每个元素构成成一个Node// 3. 将Node 放入到ArrayList中List<Node> nodes = new ArrayList<Node>();for (int value : arr) {nodes.add(new Node(value));}//我们处理的过程是一个循环的过程while(nodes.size() > 1) {//排序 从小到大Collections.sort(nodes);System.out.println("nodes =" + nodes);//取出根节点权值最小的两颗二叉树//(1) 取出权值最小的结点（二叉树）Node leftNode = nodes.get(0);//(2) 取出权值第二小的结点（二叉树）Node rightNode = nodes.get(1);//(3)构建一颗新的二叉树Node parent = new Node(leftNode.value + rightNode.value);parent.left = leftNode;parent.right = rightNode;//(4)从ArrayList删除处理过的二叉树nodes.remove(leftNode);nodes.remove(rightNode);//(5)将parent加入到nodesnodes.add(parent);}//返回哈夫曼树的root结点return nodes.get(0);}}// 创建结点类// 为了让Node 对象持续排序Collections集合排序// 让Node 实现Comparable接口class Node implements Comparable<Node> {int value; // 结点权值char c; //字符Node left; // 指向左子结点Node right; // 指向右子结点//写一个前序遍历public void preOrder() {System.out.println(this);if (this.left != null) {this.left.preOrder();}if (this.right != null) {this.right.preOrder();}}public Node(int value) {this.value = https://www.huyubaike.com/biancheng/value;}@Overridepublic String toString() {return"Node [value="https://www.huyubaike.com/biancheng/+ value +"]";}@Overridepublic int compareTo(Node o) {// TODO Auto-generated method stub// 表示从小到大排序return this.value - o.value;}}

经验总结扩展阅读


上一篇：同一趟车可以买两张票吗分段

下一篇：第一套房有房产税吗