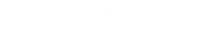岭(Ridge 线性回归大结局、 Lasso回归原理、公式推导)，你想要的这里都有( 三 ) _生活百科

根据上面的推导，在由公式\((20)\) 到 \((21)\) 是等式两遍同时乘了 \(X^TX\)的逆矩阵，但是实际情况中，矩阵的逆可能是不存在的，当矩阵 \(X^TX : n\times n\) 不是满秩矩阵的时候，即 \(r(X^TX) < n\)即 \(X^TX\) 行列式为 0时，\((X^TX)^{-1}\) 不存在。一种常见的情况是，当\(x\) 的的样本数据小于他的维数的时候，即对于 \(X\) 来说 \(n<m\)，那么\(r(X) < m\) ，又根据矩阵性质 \(r(X) = r(X^T) = r(X^TX)\)，可以得到 \(r(X^TX) < m\)，那么 \(X^TX\) 不满秩，则 \((X^TX)^{-1}\) 不存在。
对于上述 \((X^TX)^{-1}\) 不存在的情况一种常见的解决办法就是在损失函数 \(\mathcal{L(\hat{w})}\) 后面加一个\(L_2\)正则化惩罚项：
\[\mathcal{L(\hat{w})} = ||X\hat{w} - Y||_2^2 + \lambda||\hat{w}||_2^2= (X\hat{w} - Y)^T(X\hat{w} - Y) + \lambda\hat{w}^T\hat{w} \tag{22}\]则对 \(\hat{w}\) 求导有：
\[\frac{\partial \mathcal{L(\hat{w})}}{\partial \hat{w}} = 2X^TX\hat{w} - 2X^TY + 2\lambda\hat{w}= 0 \tag{23}\]\[(X^TX+\lambda E)\hat{w} = X^TY\]当 \(X^TX\) 不满秩的时候，其行列式为0，加上 \(\lambda E\)之后可以使得 \(X^TX+\lambda E\) 行列是不为0，所以 \((X^TX+\lambda E)^{-1}\)存在则：
\[\hat{w} = (X^TX+\lambda E)^{-1}X^TY \tag{24}\]除了上面提到的\(X^TX\)不满秩的情况，还有一种常见的就是数据之间的共线性的问题，它也会导致\(X^TX\)的行列式为0，即\(X^TX\)不满秩。简单来说就是数据的其中的一个属性和另外一个属性有某种线性关系，也就是说这两个属性就相当于一个属性，因为其中一个属性可以用另外一个属性线性表示。这会让模型再训练的时候导致过拟合，因为模型再训练的时候不会去关心属性之间是否具有线性关系，模型只会不加思考的去降低整个模型的损失，即\(MSE\)，这会让模型捕捉不到数据之间的关系，而只是单纯的去降低训练集的\(MSE\) 。而你如果只是单纯的去降低你训练集的\(MSE\)的时候，没有捕捉到数据的规律，那么模型再测试集上会出现比较差的情况，即模型会出现过拟合的现象。
为什么正则化惩罚项Work?上面谈到模型出现过拟合的现象，而加上\(L_2\)损失可以一直过拟合现象，我在这里简单给大家说说我得观点，不一定正确，希望可以帮助大家理解为什么\(L_2\)惩罚项可以在一定程度上抑制过拟合现象。首先看一下真实数据：

文章插图
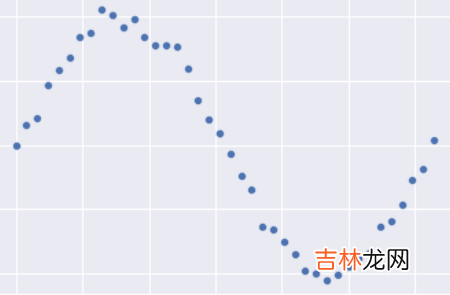
如果需要拟合的话，下面的结果应该是最好的，即一个正弦函数：

文章插图
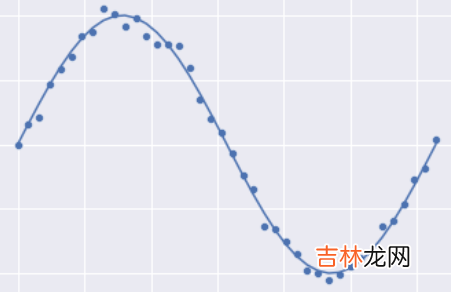
下图是一个过拟合的情况：

文章插图
我们可以观察一下它真实规律正弦曲线的之间的差异：过拟合的曲线将每个点都考虑到了，因此他会有一个非常大的缺点就是”突变“，即曲线的斜率的绝对值非常大，如：

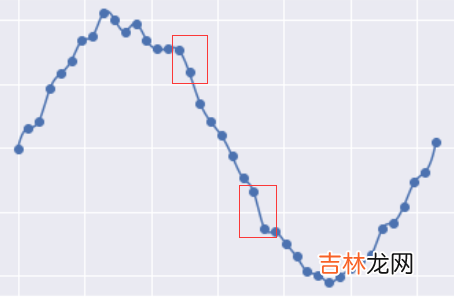
文章插图
对于一般的一次函数 \(y = ax + b\) 来说，当 \(a\) 很大的时候，斜率会很大，推广到复杂模型也是一样的，当模型参数很大的时候模型可能会发生剧烈的变化，即可能发生过拟合现象。现在我们来看为什么在线性回归中加入了一个 \(L_2\) 惩罚项会减少过拟合的现象。因为在损失函数中有权重的二范数的平方，当权重过大的时候模型的损失就会越大，但是模型需要降低损失，那么就需要降低权重的值，权重的值一旦低下来，突变的可能性就会变小，因此在一定程度上可以抑制过拟合现象。而参数 \(\alpha\) 就是来调控权重在损失中的比例，当 \(\lambda\) 越大的时候对权重惩罚的越狠，这在实际调参的过程中需要了解。后面的 \(Lasso\) 回归参数 \(\alpha\) 的意义也是相似的。